分形現象: 科學領域的“一沙一世界”

“一沙一世界”是哲學或文學領域的說法，如果從科學角度來說，要判斷一粒沙子中有沒有世界，首先需要界定“世界”的概念和范圍。

其實，在科學中也有與“一沙一世界”相似的概念——分形。擁有分形特征的圖形，其細節部分看起來和整體圖形相同或相似，比如雪花、海岸線的輪廓等。在觀賞這些圖形時，我們隻需了解部分，便可類推出其全貌，見微知著，好像一眼便由一粒沙望到了整個世界。

我們拿海岸線來舉個例子。在遙遠的澳洲大陸，大象想要探索新世界，於是沿著海岸線一直走，走了三萬多公裡，最后又回到了起點。螞蟻也踏上了探索之路，雖然中途坎坷，最終也還是回到了起點。而螞蟻卻走了五萬多公裡！

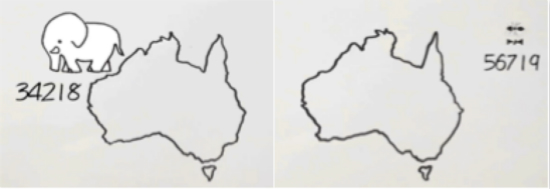
（楊默涵/繪圖）

沿同樣的路線行走，螞蟻為何如此悲催？罪魁禍首就是萬惡的海岸線。大象可以一步輕鬆邁過的彎兒，螞蟻卻隻能老老實實沿著彎兒走，隻能說，螞蟻的步子太小了。

（楊默涵/繪圖）

如果從地圖上選取一段海岸線並放大，我們會發現，這段海岸線還是和放大前一樣彎彎曲曲，這就是數學中的自相似性，即部分的結構和整體的結構是相似的。自相似性是分形圖形的主要特征。就如同《火影忍者》中綱手的蛞蝓，巨大的蛞蝓可以分成千千萬萬隻小蛞蝓，而它們與大蛞蝓完全一樣，只是體積略小一些。這幾乎完美地詮釋了自相似性的概念。

蛞蝓被大蛇纏住時，能分裂為千萬隻小蛞蝓脫身。（楊默涵/繪圖）

數學中，分形理論最為典型的例子是Koch雪花，它在體積不變的情況下，可以如下圖所示，由簡單圖形變為無限復雜的圖形。Koch雪花看起來十分抽象，但對它的研究，有助於我們更好地理解現實中的分形現象，並讓我們以科學的視角，感受“一沙一世界”的玄妙與精美。

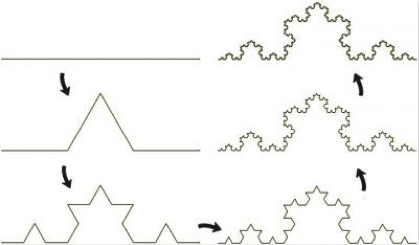
（楊默涵/繪圖）

本文由北京航空航天大學自動化科學與電氣工程學院副教授秦曾昌進行科學性把關。