分形现象: 科学领域的“一沙一世界”

“一沙一世界”是哲学或文学领域的说法，如果从科学角度来说，要判断一粒沙子中有没有世界，首先需要界定“世界”的概念和范围。

其实，在科学中也有与“一沙一世界”相似的概念——分形。拥有分形特征的图形，其细节部分看起来和整体图形相同或相似，比如雪花、海岸线的轮廓等。在观赏这些图形时，我们只需了解部分，便可类推出其全貌，见微知著，好像一眼便由一粒沙望到了整个世界。

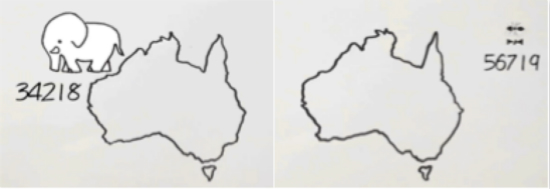
我们拿海岸线来举个例子。在遥远的澳洲大陆，大象想要探索新世界，于是沿着海岸线一直走，走了三万多公里，最后又回到了起点。蚂蚁也踏上了探索之路，虽然中途坎坷，最终也还是回到了起点。而蚂蚁却走了五万多公里！

（杨默涵/绘图）

沿同样的路线行走，蚂蚁为何如此悲催？罪魁祸首就是万恶的海岸线。大象可以一步轻松迈过的弯儿，蚂蚁却只能老老实实沿着弯儿走，只能说，蚂蚁的步子太小了。

（杨默涵/绘图）

如果从地图上选取一段海岸线并放大，我们会发现，这段海岸线还是和放大前一样弯弯曲曲，这就是数学中的自相似性，即部分的结构和整体的结构是相似的。自相似性是分形图形的主要特征。就如同《火影忍者》中纲手的蛞蝓，巨大的蛞蝓可以分成千千万万只小蛞蝓，而它们与大蛞蝓完全一样，只是体积略小一些。这几乎完美地诠释了自相似性的概念。

蛞蝓被大蛇缠住时，能分裂为千万只小蛞蝓脱身。（杨默涵/绘图）

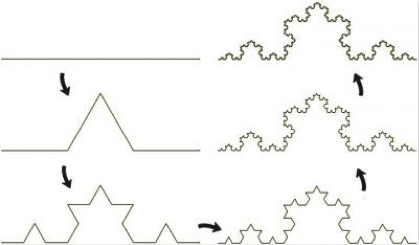
数学中，分形理论最为典型的例子是Koch雪花，它在体积不变的情况下，可以如下图所示，由简单图形变为无限复杂的图形。Koch雪花看起来十分抽象，但对它的研究，有助于我们更好地理解现实中的分形现象，并让我们以科学的视角，感受“一沙一世界”的玄妙与精美。

（杨默涵/绘图）

本文由北京航空航天大学自动化科学与电气工程学院副教授秦曾昌进行科学性把关。